อนุกรม สถิติสำหรับข้อมูลประหลาด
อนุกรม สถิติสำหรับข้อมูลประหลาด
หากพิจารณาถึงข้อมูลเพื่อใช้ในการประมวลผล เช่น การสำมะโนประชากร การตรวจสุขภาพประจำปี หรือการสำรวจความพึงพอใจ มักจะมีการมองในลักษณะแบ่งออกเป็นข้อมูลเชิงคุณภาพ (qualitative data) และข้อมูลเชิงปริมาณ (quantitative data) ดังผังที่ปรากฏในรูปที่ 1 โดยมีการตีความมักแบ่งจากวิธีการประมวลผลข้อมูลสำหรับการใช้งานทางสถิติ1
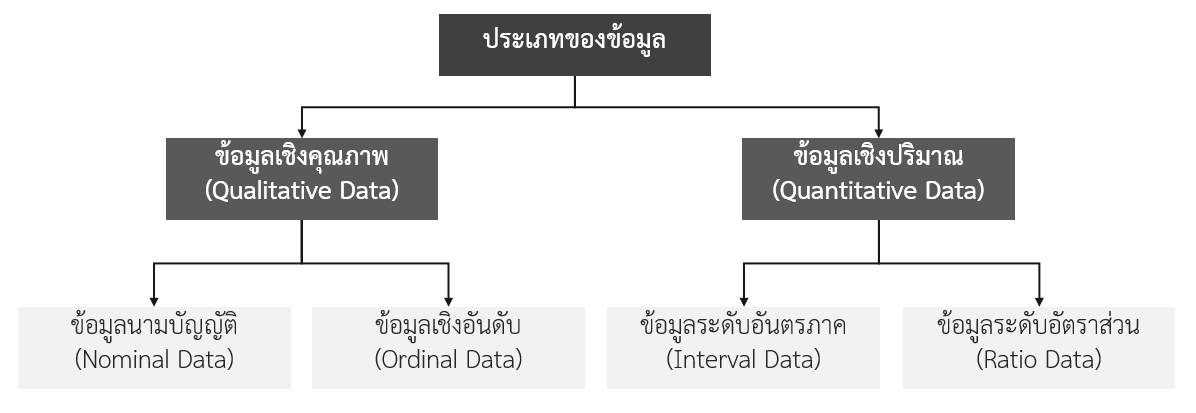
รูปที่ 1 การจัดแบ่งหมวดของข้อมูลอย่างพื้นฐานซึ่งเป็นการแบ่งชนิด 4 รูปแบบ
บทความนี้จะลงมาเจาะลึกเกี่ยวกับประวัติศาสตร์และการตีความเชิงปรัชญาเกี่ยวกับประเภทข้อมูลทางสถิติทั้ง 4 รูปแบบที่ปรากฏกันในตำราเรียนว่ามาจากไหนและมีอะไรเป็นข้อกังวลบ้าง
การตีความเกี่ยวกับชนิดของข้อมูลตามอย่างทั่วไปที่มี 4 รูปแบบ ประกอบด้วย ข้อมูลนามบัญญัติ (categorical data) ข้อมูลเชิงอันดับ (ordinal data) ข้อมูลระดับอันตรภาค (interval data) และข้อมูลระดับอัตราส่วน (ratio data) เริ่มต้นจากงานวิจัยของสแตนลีย์ สมิธ สตีเฟนส์ (Stanley Smith Stevens) นักจิตวิทยาชาวอเมริกันผ่านงานเขียนของเขาที่ชื่อ On the Theory of Scales and Measurement (ว่าด้วยทฤษฎีหน่วยวัดและการวัด) ในปี ค.ศ. 1946 (พ.ศ. 2489)2

รูปที่ 2 สแตนลีย์ สมิธ สตีเฟนส์
(Stanley Smith Stevens, ค.ศ. 1906-1973; พ.ศ. 2449-2517)
อ้างอิงรูปภาพจาก Miller G.A. (1975), Stanley Smith Stevens 1906-1973, National Academy of Science (สามารถเข้าถึงได้ที่นี่)
สแตนลีย์ สมิธ สตีเฟนส์เป็นใคร
โดยเบื้องต้นแล้วสแตนลีย์ สมิธ สตีเฟนส์ (Stanley Smith Stevens) เป็นนักจิตวิทยาชาวอเมริกัน ซึ่งเป็นผู้ก่อตั้งกลุ่มวิจัยจิตสวนศาสตร์ (อ่านว่า จิด-ตะ-สะ-วะ-นะ-สาด, Psychoacoustics: หมายถึงศาสตร์เกี่ยวกับจิตวิทยาของเสียง) ของมหาวิทยาลัยฮาร์เวิร์ดตามที่กองทัพอากาศสหรัฐฯ ต้องการให้มีการพัฒนาการสื่อสารระหว่างเครื่องบินรบที่เสียงดังที่ระดับการบินที่สูงมากในสมัยสงครามโลกครั้งที่ 2 (1940) โดยทดลองระดับความรู้เรื่องในการสื่อสารด้วยการดูปัจจัยทางเสียง ความดัน และความล้า
อ้างอิงจากข้อมูลวิจัยของสตีเฟนส์ในฐานข้อมูล Scopus จะพบว่าเขามีจำนวนงานวิจัยและหนังสือทั้งสิ้น 99 ชิ้น เขามีผลงานมากที่สุดในช่วงทศวรรษ ค.ศ. 1960 (ประมาณช่วง พ.ศ. 2500) จากงานระบุความรู้สึกด้วยระดับความดังและความสว่างอ้างอิงจากความเข้มพลังงานของเสียงและแสงตามลำดับดังรูปที่ 3 หรืออาจเรียกได้ว่า เขาเป็นนักจิตวิทยาที่พยายามหาความเชื่อมโยงระหว่างความรู้สึกของมนุษย์กับฟิสิกส์ จึงอาจเป็นเหตุที่ไม่ประหลาดใจนัก หากเขาเป็นผู้ที่จัดประเภทข้อมูลทั้ง 4 แบบเพื่อการทำงานด้านสถิติ สืบเนื่องจากเขาเป็นผู้ที่สนใจเกี่ยวกับระดับของค่าทางกายภาพในงานวิจัยตลอดชีวิตการทำงานของเขา
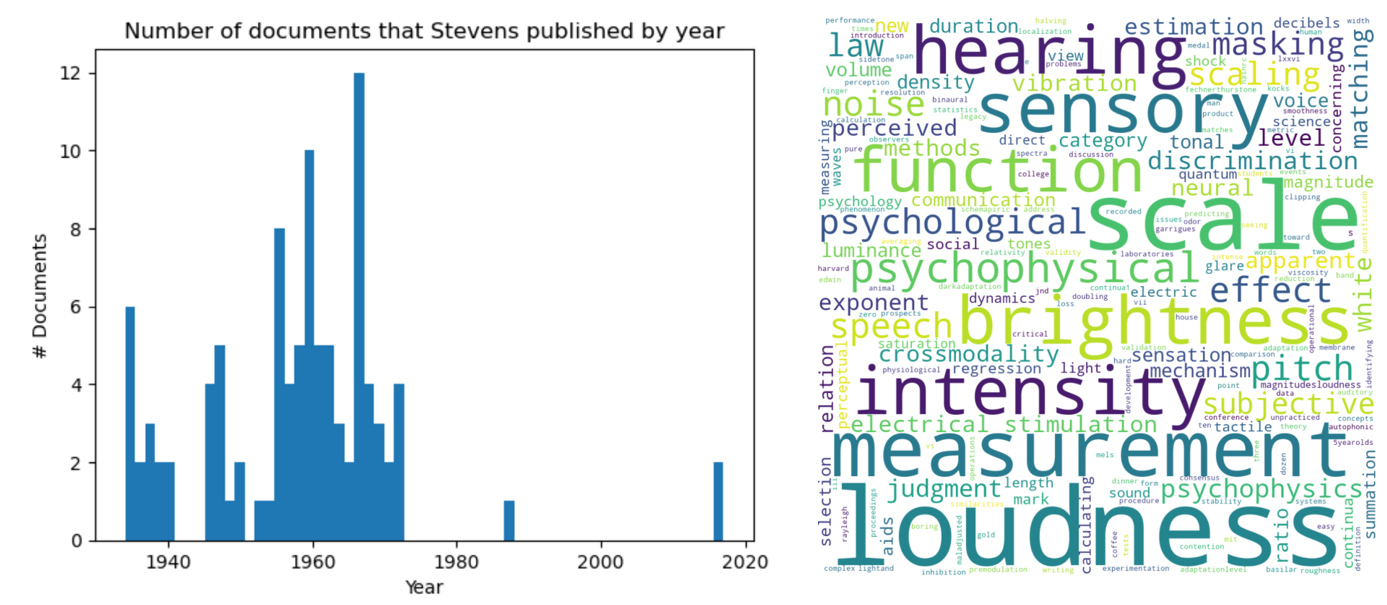
รูปที่ 3 ผลงานวิจัยและหนังสือโดยรวมของ Stanley Smith Stevens โดยพิจารณาจากช่วงเวลาในการตีพิมพ์ (ซ้าย) และแนวโน้มหัวข้อวิจัยจาก WordCloud ของหัวข้อผลงาน (ขวา)
โดยงานวิจัยที่ได้อ้างอิงมากที่สุดเป็น 5 อันดับแรก ประกอบด้วยงานวิจัยดังนี้
| ผู้เขียน | หัวข้อผลงาน (ปีที่ตีพิมพ์) | จำนวนการอ้างอิง |
|---|---|---|
| Stevens S.S. | On the theory of scales of measurement (ค.ศ. 1946; พ.ศ. 2489) | 2,955 |
| Stevens S.S. | On the psychophysical law (ค.ศ. 1957; พ.ศ. 2500) | 2,298 |
| Stevens S.S.; Volkmann J.; Newman E.B. | A Scale for the Measurement of the Psychological Magnitude Pitch (ค.ศ. 1937; พ.ศ. 2480) | 742 |
| Stevens S.S.; Galanter E.H. | Ratio scales and category scales for a dozen perceptual continua (ค.ศ. 1957; พ.ศ. 2500) | 611 |
| Stevens S.S. | To honor Fechner and repeal his law (ค.ศ. 1961; พ.ศ. 2504) | 573 |
ตารางที่ 1 ผลงานวิจัยและหนังสือของ Stanley Smith Stevens ที่ได้รับการอ้างอิงจากผลงานชิ้นอื่น (citation) มากที่สุดอ้างอิงจากฐานข้อมูล Scopus
- ฐานข้อมูล Scopus เป็นฐานข้อมูลวิจัยที่ใช้สำหรับในการดูบทคัดย่อและการอ้างอิงของงานวิจัยต่าง ๆ (abstract and citation database หรืออาจเรียกว่า citation index) ซึ่งใช้เพื่อค้นหาความคิดและความเข้าใจเนื้อหางานวิจัยในอดีต
- รหัสต้นฉบับสำหรับการสร้างรูปภาพและตารางข้างต้นสามารถค้นหาได้ที่นี่
งาน On the Theory of Scales and Measurement (ค.ศ. 1946; พ.ศ. 2489) กล่าวถึงอะไร

รูปที่ 4 งาน On the Theory of Scales and Measurement (ค.ศ. 1946; พ.ศ. 2489) ซึ่งถูกตีพิมพ์ในวารสาร Science หนึ่งในวารสารที่มีชื่อเสียงที่สุดจนถึงปัจจุบัน
งานชิ้นนี้เกิดขึ้นเพื่อแก้ปมปัญหา "การวัด" ในทางจิตวิทยา
ตลอดระยะเวลานับตั้งแต่ช่วงการปฏิวัติวิทยาศาสตร์ การวิเคราะห์เชิงปริมาณ (Quantitative analysis) ทำให้ปรากฏการณ์ธรรมชาติ เช่น การเคลื่อนที่ของวัตถุ ปฏิกิริยาเคมี สามารถอธิบายและคำนวณโดยใช้เครื่องมือทางคณิตศาสตร์ได้ ซึ่งการวิเคราะห์เชิงปริมาณถูกมองว่าเป็นรากฐานของวิทยาศาสตร์ ทว่าการอธิบายปรากฏการณ์ธรรมชาติหลายอย่างสามารถทำการวิเคราะห์เชิงปริมาณได้ ปรัชญาของความคิด (Philosophy of mind) หรือจิตวิทยา กลับเป็นการศึกษาปรากฏการณ์ธรรมชาติหนึ่งที่ถูกถกเถียงอย่างมากว่าสามารถเป็นวิทยาศาสตร์ได้หรือไม่
1) การทำให้จิตวิทยาเป็นวิทยาศาสตร์สามารถทำได้
เริ่มต้นจากการเปิดประเด็นโดยอิมมานูเอล คานท์ (Immanuel Kant) (ค.ศ. 1724-1804; พ.ศ. 2267-2347) นักปรัชญาชาวเยอรมันได้เขียนสรุปไว้ในงานเขียนที่ชื่อว่า Metaphysische Anfangsgründe der Naturwissenschaft (รากฐานอภิปรัชญาของวิทยาศาสตร์ธรรมชาติ) โดยใช้ทัศนะแบบนิวตันในการมองวิทยาศาสตร์ธรรมชาติมองซึ่งสรุปว่า
“จิตวิทยาไม่สามารถเป็นวิทยาศาสตร์ได้ เพราะจิตวิทยาไม่สามารถควบคุมเป็นการทดลองและไม่สามารถใช้คณิตศาสตร์เพื่ออธิบายปรากฏการณ์ได้ จึงเป็นได้เพียงศาสตร์ที่มีความเป็นระบบ (systematic art) เท่านั้น3”
ในเวลาต่อมา กุสตาฟ เฟกเนอร์ (Gustav Fechner, ค.ศ. 1801-1887; พ.ศ. 2344-2430) นักจิตวิทยาชาวเยอรมันและนักปรัชญาท่านอื่น ๆ เช่น เอิร์นส ไฮน์ริก วีเบอร์ (ค.ศ. 1795-1878; พ.ศ. 2338-2421) แพทย์ชาวเยอรมันและ โยฮันน์ เฟรดเดอริก เฮอร์บาร์ต (ค.ศ. 1776-1841; พ.ศ. 2319-2384) นักจิตวิทยาชาวเยอรมันที่เสนองานใกล้เคียงกันอย่างจิตวิทยากายภาพ (Psychophysics) อันเป็นที่มาของกฎของเฟกเนอร์ (Fechner’s law หรืออาจคุ้นเคยในนามของกฎของวีเบอร์; Weber’s law) ซึ่งเป็นกฎว่าด้วยความดังของเสียงที่ผู้คนได้ยินขึ้นอยู่กับฟังก์ชันลอการิทึมของความเข้มเสียง นับว่าเป็นการเปลี่ยนมุมมองจากที่จิตวิทยาเป็นศาสตร์ที่มีความเป็นระบบกลายเป็นวิทยาศาสตร์อันเป็นลักษณะความแย้งตามที่คานท์ได้เสนอไว้ในที่สุด
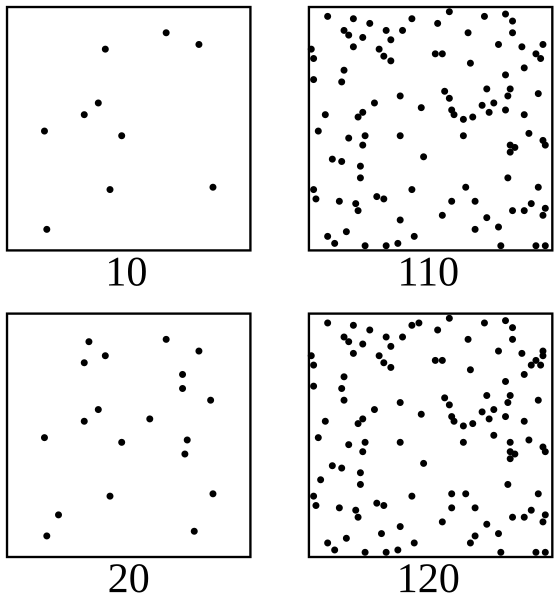
รูปที่ 5 หากเราแสดงถึงกฎของวีเบอร์-เฟกเนอร์ (Weber-Fechner Law) จะเห็นได้ว่าจากภาพ เราจะรู้สึกว่ามีจำนวนจุดเพิ่มขึ้นเป็นสัดส่วนร้อยละที่เพิ่มขึ้น เช่นเราจะรู้สึกว่าจำนวนจุดที่เพิ่มขึ้น 10 จุดจากเดิมที่มี 10 จุด แตกต่างกว่า จำนวนจุดที่เพิ่มขึ้น 10 จุดจากเดิมที่มี 110 จุด (อ้างอิง: An illustration of the Weber-Fechner law - MrPomidor)
เฟกเนอร์กล่าวถึงอะไรเกี่ยวกับจิตวิทยากายภาพ

รูปที่ 5 หนังสือ Elemente der Psychophysik (1860) โดยกุสตาฟ ธีโอดอร์ เฟกเนอร์ (Gustav Theodor Fechner)
กุสตาฟ เฟกเนอร์ ได้เขียนหนังสือภาษาเยอรมัน Elemente der Psychophysik (มูลบทจิตวิทยากายภาพ) ซึ่งกล่าวถึงการอธิบายจิตวิทยาของวัตถุกายภาพผ่านกฎของวีเบอร์ (Weber’s law) เช่น ความสว่าง ความดังของเสียง น้ำหนัก อุณหภูมิ การสัมผัสและการมองเห็น ว่าด้วยปริมาณต่ำสุดที่สามารถรับรู้ได้ (threshold) โดยอธิบายทั้งในเรื่องทฤษฎีพร้อมแบบจำลองคณิตศาสตร์ที่เกี่ยวข้องและการทดลองซึ่งกล่าวถึงการวัดพร้อมการมองความคลาดเคลื่อนในลักษณะที่เป็นการแจกแจงปกติ (Normal distribution)4

รูปที่ 6 เนื้อหาใน Elemente der Psychophysik ได้กล่าวถึงการแจกแจงปกติซึ่งกล่าวถึงการมองความคลาดเคลื่อนในการทดลอง (อ้างอิงหน้า 106)
ทว่าการค้านข้อเสนอของนักจิตวิทยาในช่วงนั้นมิได้เกิดอย่างไร้บริบทแต่อย่างใด ซึ่งเราสามารถสรุปเหตุที่ทำให้จิตวิทยาสามารถเป็นวิทยาศาสตร์ได้ว่าเกิดขึ้นจากสาเหตุ 2 ประการ คือ
- พัฒนาการทางสังคมที่อยู่ในระหว่างช่วงรอยต่อระหว่างการปฏิวัติอุตสาหกรรมครั้งที่ 1 (ประมาณ ค.ศ. 1760-1840; พ.ศ. 2300-2380) กับ การปฏิวัติอุตสาหกรรมครั้งที่ 2 (ประมาณ ค.ศ. 1870-1914; พ.ศ. 2410-2457) ซึ่งเริ่มมีการศึกษาทางจิตวิทยาเพราะเหตุของการเปลี่ยนแปลงไปของสภาพสังคมที่มีความเป็นเมืองเพื่อรองรับงานอุตสาหกรรมที่มากขึ้นในสหพันธรัฐเยอรมนี นับตั้งแต่การดูโหงวเฮ้ง (Physiognomy) และการพยากรณ์โรคจากลักษณะกระโหลกศีรษะ (Phrenology) เพื่อเดาใจของผู้นั้น5, 6 รวมถึงจิตวิทยากายภาพของเฟกเนอร์ด้วย
- การศึกษาต่าง ๆ ทั้งวิทยาศาสตร์แท้และวิทยาศาสตร์เทียมสามารถเกิดขึ้นได้เนื่องจากเสรีภาพทางวิชาการที่อยู่ภายในเยอรมนีผ่านแนวคิด “Lernfreiheit” (เสรีภาพในการเรียน) และ “Lehrfreiheit” (เสรีภาพในการสอน) ทำให้เกิดพัฒนาการและความก้าวหน้าทางวิทยาศาสตร์ภายในเยอรมนีช่วงสมัยนั้น เพื่อให้เกิดข้อถกเถียงและบทพิสูจน์สุดท้ายอย่างเป็นเหตุเป็นผล ทำให้การท้าทายข้อเสนอของคานท์เกี่ยวกับจิตวิทยาไว้ในอดีตสามารถกระทำได้7
2) ปัญหาเรื่องการวัดในทางจิตวิทยา
หลังจากที่มีการเสนอทฤษฎีจิตวิทยากายภาพขึ้นในช่วงปลายศตวรรษที่ 19 อย่างที่เฟกเนอร์และคณะได้ทำทฤษฎีขึ้นพร้อมกับวิธีการวัดในการทดลองขึ้น วงการจิตวิทยาได้ทำการทดลองเชิงปริมาณพร้อมเสนอวิธีการวัดเป็นจำนวนมากโดยปราศจากข้อกังวล จนกระทั่งในปี ค.ศ. 1932 (พ.ศ. 2475) สมาคมเพื่อความก้าวหน้าทางวิทยาศาสตร์แห่งบริเตน (British Association for the Advancement of Science) ได้ตั้งข้อกังวลอย่างชัดเจนเกี่ยวกับการวัดในทางจิตวิทยา8
สมาคมเพื่อความก้าวหน้าทางวิทยาศาสตร์แห่งบริเตนได้จัดงานประชุมประจำปี ค.ศ. 1932 ในงานห้องที่ A (วิทยาการคณิตศาสตร์และวิทยาศาสตร์กายภาพ) ร่วมกับห้องที่ J (จิตวิทยา) ในหัวข้อเรื่อง The quantitative relation of physical stimuli and sensory events (ความสัมพันธ์เชิงปริมาณระหว่างการกระตุ้นเชิงกายภาพและเหตุการณ์รับรู้ความรู้สึก) โดยปัญหาที่นักจิตวิทยาที่อยู่ในหัวข้อการเสวนาได้ระบุปัญหาเกี่ยวกับความเป็นปัจเจก (subjective) ในเรื่องระดับความรู้สึกของมนุษย์ที่ก่อให้เกิดความคลาดเคลื่อนในการวัดซึ่งอาจก่อปัญหาในการสรุปออกมาเป็นทฤษฎี แต่ก็ยังเห็นถึงความจำเป็นในการทดลองทางจิตวิทยาให้มีการวัดเป็นตัวแปรเชิงปริมาณ9 จึงได้ตั้งประเด็นการศึกษาสุดท้ายเกี่ยวกับการวัดว่าควรเป็นในลักษณะใด
ในงาน On the Theory of Scales and Measurement ได้ประกาศสิ่งสำคัญในการจัดทำการทดลองและทฤษฎีทางจิตวิทยาอยู่ทั้งสิ้น 2 สิ่ง ประกอบด้วย นิยามของการวัด และ การจัดแบ่งประเภทของข้อมูลซึ่งแบ่งออกเป็น 4 ประเภทดังที่กล่าวไว้ในตอนแรก
1) การนิยามคำว่า “การวัด”
สตีเฟนส์ได้ระบุปัญหาที่สำคัญในวงการจิตวิทยา ณ ขณะนั้น คือ “ความหมายของการวัดหมายถึงอะไร” ซึ่งมีประเด็น10 ว่าถ้าไม่มีการให้ความหมายการบวกในเชิงความรู้สึก กฎที่กำหนดค่าตัวเลขในตัวแปรเชิงปริมาณจะไม่จริงและไม่มีความหมายใด ๆ ทั้งสิ้น สตีเฟนส์จึงทำการสรุปคำว่า “การวัด” ว่าเกี่ยวข้องกับการกำหนดโครงสร้างทางพีชคณิตของตัวแปรนั้นซึ่งก็คือกฎ โดยสรุปเป็นนิยามสมบูรณ์ได้ดังนี้
การวัด หมายถึง “การให้ค่าตัวเลขกับสิ่งของเพื่อการแสดงแทนถึงความจริงและสัญกรณ์ของมัน” (The assignment of numerals to things so as to represent facts and conventions about them.)
— สแตนลีย์ สมิธ สตีเฟนส์11
สตีเฟนส์ได้กล่าวว่าโครงสร้างทางพีชคณิตที่เกี่ยวข้องกับตัวแปรความรู้สึกในทางจิตวิทยาว่าเป็นอย่างไรให้ดูจากสมสัณฐาน (isomorphism) ที่ส่งจากตัวแปรเชิงความรู้สึกไปยังวัตถุทางคณิตศาสตร์ ซึ่งในงานวิจัยได้แบ่งประเภทข้อมูลออกเป็น 4 ประเภทด้วยลักษณะของสมสัณฐาน
2) ประเภทของข้อมูล
โดยในตารางที่ 2 แถวข้อมูลที่อยู่ด้านล่างจะมีคุณสมบัติตามด้านบนด้วยเช่นกัน อาทิ ข้อมูลระดับอัตราส่วนสามารถใช้คุณสมบัติของข้อมูลระดับอันตรภาค ข้อมูลเชิงอันดับ และข้อมูลนามบัญญัติมากระทำการวิเคราะห์เชิงสถิติได้ ซึ่งถ้าหากเจาะรายละเอียด ข้อมูลแต่ละประเภทมีรายละเอียดเพิ่มเติมดังนี้
| ประเภทข้อมูล | ตัวดำเนินการประจักษ์ | สถิติที่สามารถทำได้ |
|---|---|---|
| ข้อมูลนามบัญญัติ (Nominal data) | การหาความเท่ากัน | จำนวนเคส, ฐานนิยม หรือสหสัมพันธ์การณ์จร (Contingency correlation) |
| ข้อมูลเชิงอันดับ (Ordinal data) | การหาการมากหรือน้อยกว่า | มัธยฐาน, เปอร์เซนไทล์ |
| ข้อมูลระดับอันตรภาค (Interval data) | การหาความเท่ากันของช่วงหรือความแตกต่าง | ค่าเฉลี่ย, ส่วนเบี่ยงเบนมาตรฐาน, สหสัมพันธ์อันดับขั้น (Rank-order correlation), สหสัมพันธ์โมเมนต์การคูณ (Product-moment correlation) |
| ข้อมูลระดับอัตราส่วน (Ratio data) | การหาความเท่ากันของอัตราส่วน | สัมประสิทธิ์การแปรผัน (Coefficient of variation) |
ตารางที่ 2 ลักษณะประเภทของข้อมูลตามที่สตีเฟนส์ได้จัดจำแนกในบทความของเขา12
ข้อมูลนามบัญญัติ (Nominal Data): โดยปกติแล้ว ข้อมูลนามบัญญัติจะลักษณะเป็นชื่อสิ่งของหรือหมวดประเภทอื่นใด โดยการให้ค่าตัวเลขแก่ชื่อสิ่งของเหล่านี้จะคล้ายคลึงการทำรหัส (Data encoding) ก็มิปาน
ข้อมูลลำดับ (Ordinal Data): มีลักษณะเป็นลำดับสามารถเรียงมากหรือน้อยได้ ซึ่งในบทความได้ยกตัวอย่างการคงสภาพลำดับ หากแปลอีกนัยหนึ่งทางคณิตศาสตร์ จะหมายถึง อันดับอย่างอ่อน (Weak ordering) ตามนิยาม 1
นิยาม 1 (อันดับอย่างอ่อน, weak ordering). พิจารณา $(A, \leq)$ เป็นเซตที่มีความสัมพันธ์ หาก $\leq$ เป็นความสัมพันธ์ที่เป็นอันดับอย่างอ่อนจะต้องมีคุณสมบัติดังต่อไปนี้
- สมบัติการถ่ายทอด: สำหรับทุก $x, y, z \in A$ หาก $x \leq y$ และ $y \leq x$ แล้ว $x \leq z$
- สมบัติการเชื่อมต่อกันอย่างบริบูรณ์ (Strong connectedness): สำหรับทุก สำหรับทุก $x, y \in A$ จะต้องให้ $x \leq y$ หรือ $y \leq x$
ซึ่งเราจะพบว่าอันดับอย่างอ่อนเปรียบเสมือนกับการเทียบลำดับที่สามารถเรียงว่าวัตถุใดมากกว่าหรือน้อยกว่าวัตถุใด มีลักษณะเป็นการเรียงลำดับสายเดียว แต่การเทียบลำดับเท่ากันอาจมีได้หลายวัตถุ เช่น คะแนนในการแข่งขันเทอร์นาเมนต์ที่สามารถมีอันดับเดียวกันได้หลายคน/ทีม
ข้อมูลระดับอันตรภาค (Interval data): ข้อมูลสามารถหาความแตกต่างระหว่างวัตถุได้ เช่น อุณหภูมิ แต่หากไม่จำเป็นต้องหาความหมายของศูนย์ที่แท้จริง ซึ่งอาจมองว่าศูนย์เป็นค่าอ้างอิงก็ได้ ยกตัวอย่างในกรณี 0 องศาเซลเซียส หมายถึง อุณหภูมิที่น้ำเปลี่ยนสถานะระหว่างของเหลวกับของแข็ง ซึ่งไม่มีความจำเป็นต้องระบุว่า “ความไม่มี” อยู่ที่จุดใดโดยสากล
ข้อมูลระดับเชิงอัตราส่วน (Ratio data): ข้อมูลที่สามารถระบุอัตราส่วนได้ เช่น ปริมาตร อุณหภูมิสัมบูรณ์ (ในหน่วยเคลวิน: K) หรือหน่วยอื่น ๆ ที่มีลักษณะเป็นฟิสิกส์ที่แบ่งเป็นหน่วยสากล (International System of Units): SI Unit) และหน่วยอนุพันธ์ (Derived unit เช่น เดซิเบล)
บทวิจารณ์เกี่ยวกับการแบ่งประเภทข้อมูลของสตีเฟนส์
จากบทความของสตีเฟนส์เกี่ยวกับการแบ่งประเภทของข้อมูล นักวิจัยได้นำการแบ่งประเภทลักษณะนี้ไปใช้ในตำราเรียนสถิติเป็นอย่างมาก13, 14, 15 เป็นตัวอย่าง แต่ก็มีนักวิจัยบางส่วนเช่นกันที่มีการโต้เถียงเกี่ยวกับเรื่องนี้ในหลายประเด็น โดยได้สรุปออกมาเป็นประเด็นดังนี้16
- การเลือกวิธีการทางสถิติที่สามารถใช้วิธีการเดียวกันในประเภทข้อมูลเดียวกันได้ทั้งหมด จากงานของสตีเฟนส์ที่ระบุสถิติที่สามารถใช้ในการวิเคราะห์ได้ในตารางที่ 1 เป็นเรื่องอันตรายอย่างยิ่ง17
- เกณฑ์การจัดแบ่งข้อมูลเพียง 4 ประเภทของสตีเฟนส์มีความจำกัดกับข้อมูลในโลกจริงมากเกินไป17
- การจำกัดของสตีเฟนส์อาจทำให้เสียรูปลักษณ์ของข้อมูลโดยการเรียงลำดับและอาจทำให้เกิดการจัดเรียงข้อมูลในการทดสอบทางสถิติไม่อิงพารามิเตอร์โดยไม่จำเป็น17
- นิยามของสตีเฟนส์ที่กล่าวถึงการวัดว่าจะต้องสามารถให้ความหมายได้โดยสมบูรณ์เสมอไป การทำให้ความหมายไม่สมบูรณ์เกิดขึ้นเพื่อให้นักวิจัยสามารถเข้าใจถึงปัญหาในการวัดสำหรับการทดลองนั้นได้18
กระนั้นเอง เค้าโครงของสตีเฟนส์ก็ยังถูกใช้ในการหาความผิดปกติได้อยู่ดี โดยนำความหมายมาใช้ในการหาความไม่สมเหตุสมผลของข้อมูล หากเพียงว่าให้ดูความเป็นมาและวิธีการที่ได้มาซึ่งข้อมูลแทนที่การหาวิธีการทางสถิติในการทดสอบข้อมูลจากการดูเพียงประเภทของข้อมูลเพียงเท่านั้น
การนำเสนอการแบ่งประเภทข้อมูลนอกเหนือจากของสตีเฟนส์ยังมีแบบอื่น ๆ เช่น
- Mosteller and Tukey (1977)19: แบ่งข้อมูลออกเป็น ชื่อ (Names) เกรด (Grades) ลำดับขั้น (Ranks) อัตราเศษส่วน (Counted fractions) การนับ (Counts) จำนวน (Amounts) และยอดคงเหลือ (Balances)
- Chrisman (1998)20: ได้จัดแบ่งประเภทข้อมูลในทางการทำแผนที่และภูมิสารสนเทศศาสตร์ออกเป็นนามบัญญัติ (Nominal) เกรด (Graded membership) ลำดับ (Ordinal) อันตรภาค (Interval) อันตรภาคแบบลอการิทึม (Log-interval) อัตราส่วน (Extensive ratio) อัตราส่วนแบบวัฏจักร (Cyclic ratio: กล่าวถึงข้อมูลแบบวงกลม) อัตราส่วนอนุพันธ์ (Derived ratio: อัตราส่วนที่มาจากการคำนวณด้วยฟังก์ชันอีกทอดหนึ่ง) การนับ (Counts) และสัดส่วน 0-1 (Absolute) นอกจากนี้แล้วยังมีการแบ่งวัตถุออกเป็นวัตถุเดี่ยวกับวัตถุที่มีความสัมพันธ์เครือข่าย (Attribute control) และแบ่งเงื่อนไขกำกับเชิงพื้นที่ (Spatial control) อีกด้วย
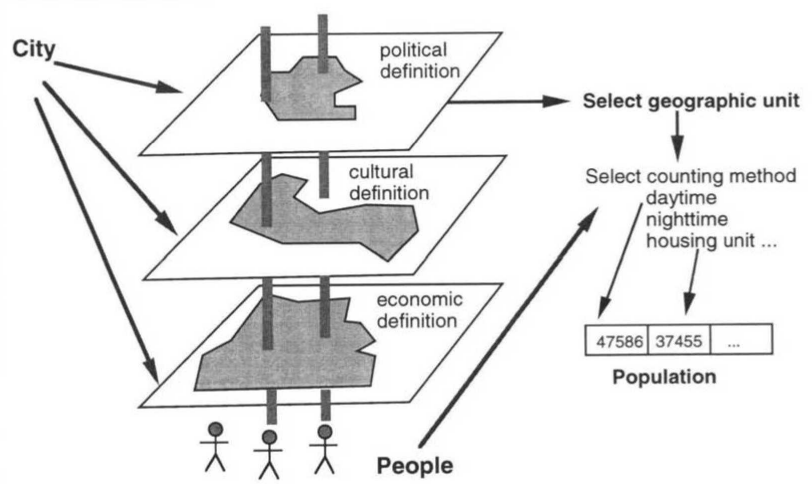
รูปที่ 7 แรงบันดาลใจในการจัดประเภทของข้อมูลของ Chrisman (1998)21
ข้อมูลประหลาด: ข้อมูลที่ไม่ค่อยถูกกล่าวถึงในสถิติแต่มีตัวอย่างในการใช้จริง
เราจะพบว่าก่อนหน้านี้ ข้อมูลแต่ละประเภทที่ถูกจำแนกออกมาล้วนเป็นข้อมูลที่เราคุ้นเคยกันในชีวิตประจำวันและงานทั่วไปของการวิเคราะห์ข้อมูลทั้งสิ้น ทว่ากลับมีข้อมูลบางชนิดที่ไม่สามารถจัดจำแนกอยู่ในหมวดประเภทใดได้เลย ซึ่งส่งผลต่อทฤษฎีการวิเคราะห์ข้อมูลทางสถิติของข้อมูลประเภทเหล่านี้ที่ต้องมีการแปลงให้เหมาะสม เราจะนำมาแสดงเป็นตัวอย่างดังต่อไปนี้ซึ่งเป็นข้อมูลที่มีการใช้ในชีวิตจริง พร้อมเสนอทฤษฎีทางสถิติของข้อมูลเหล่านั้นผ่านตอนถัด ๆ ไป
ความประหลาดแบบที่ 1: เรขาคณิตของข้อมูลที่ประหลาด
โดยปกติแล้ว ข้อมูลที่ใช้ในการวิเคราะห์สถิติมักมีโครงสร้างเหมือนกับจำนวนจริง ($\mathbb{R}$ หรืออาจมีขอบเขตบน/ล่างกำกับ) และจำนวนนับ ($\mathbb{N}_0 := \mathbb{N} \cup \lbrace 0\rbrace$) ยกตัวอย่างในกรณีทั่วไปดังนี้
- ข้อมูลที่มีโครงสร้างเหมือนจำนวนนับ (ข้อมูลวิยุตหรือข้อมูลไม่ต่อเนื่อง: Discrete data) เช่น ราคาสินค้าที่ใช้ตามสกุลเงินจริง22 คะแนนในการสอบ จำนวนสินค้า
- ข้อมูลที่มีโครงสร้างเหมือนจำนวนจริง (ข้อมูลต่อเนื่อง: Continuous data) เช่น ความสูง น้ำหนัก ความดังของเสียง
แต่หากว่าข้อมูลทางสถิติอาจอยู่บนปริภูมิอื่นซึ่งมีโครงสร้างทางเรขาคณิตที่ไม่อาจใช้เครื่องมือที่ใช้ในปริภูมิจำนวนนับและจำนวนจริง โดยปริภูมิอื่นอาจมีปริภูมิดังต่อไปนี้
1.1 ข้อมูลเชิงทิศทาง (Directional Data)

รูปที่ 8 ธงลม (Windsock) ท่อทรงกรวยผ้าซึ่งมีไว้ในการระบุความเร็วและทิศทางของลม มักอยู่ในสนามบินและโรงงานเคมี
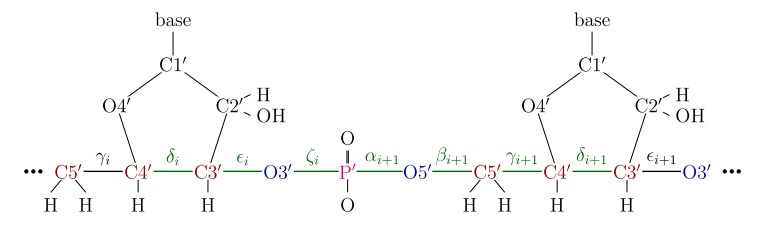
รูปที่ 9 การวิเคราะห์โครงสร้างโมเลกุลจะดูจากมุมสองหน้า (dihedral angle) และความยาวพันธะของโมเลกุล (Bond length) ซึ่งความยาวพันธะจะค่อนข้างคงที่ แต่มุมสองหน้าจะไม่คงที่ ซึ่งเป็นที่มาของการใช้สถิติเชิงทิศทางในการวิเคราะห์
ข้อมูลเชิงทิศทางอยู่บนพื้นฐานจากลักษณะทางเรขาคณิตที่เป็นคาบชัดเจนหรือปริภูมิการเคลื่อนที่ที่เป็นไปได้ (Configuration space) ของวัตถุมีลักษณะเป็นแมนิโฟลด์ปิด (Closed manifold)23 เช่น ทรงกลม (Sphere) ทอรัสที่มีจำนวน $g$ รู ($g$-Torus) หรือรูปทรงอื่น ๆ ซึ่งประโยชน์ในการใช้ข้อมูลเชิงทิศทางสามารถยกตัวอย่างได้ดังนี้
- ข้อมูลด้านสิ่งแวดล้อม: มักมีรูปลักษณ์เป็นวงกลมหรือทรงกลม เช่น
- ข้อมูลกระแสลมกระแสสมุทร โดยนำไปใช้ในการระบุหาแนวโน้มของทิศทาง ซึ่งนำไปใช้ในการหาทิศทางของพายุหรือการพาของมลพิษทางอากาศที่จะเข้ามาในอนาคตได้ อันเป็นปัจจัยพื้นฐานในการทำระบบเฝ้าระวังเตือนภัยล่วงหน้า (Early warning systems)24
- ข้อมูลด้านนิเวศวิทยา เช่น การดูแนวโน้มการบินอพยพของนกเมืองหนาว ซึ่งไว้ใช้ในการคาดการณ์การเปลี่ยนแปลงสภาพภูมิอากาศได้25
- ข้อมูลด้านธรณีวิทยา เช่น ข้อมูลสถิติสนามแม่เหล็กโลกที่ดูตำแหน่งของขั้วเหนือและขั้วใต้ภายใต้พิกัดทรงกลม25
- ข้อมูลทางชีวโมเลกุล: มักมีรูปลักษณ์เป็นทรงทอรัสด้วยเหตุของการวางมุมของโมเลกุล (Dihedral angle) มีลักษณะเป็นอิสระต่อกัน ซึ่งสามารถนำไปใช้ในการทำนายรูปลักษณ์ของโมเลกุลขนาดใหญ่ที่แท้จริงได้26, 27
- ข้อมูลเวลา: สามารถนำสถิติข้อมูลเชิงทิศทางมาใช้อธิบายการแจกแจงความน่าจะเป็นของการเกิดเหตุการณ์ในช่วงเวลา ซึ่งสามารถนำมาใช้ได้ทั้งในปรากฏการณ์ธรรมชาติ28 และปรากฏการณ์ทางสังคม29 เพื่อวิเคราะห์แนวโน้มเชิงฤดู (seasonal trend)
โดยหนังสือตำราหรือบทความที่กล่าวถึงการวิเคราะห์สถิติสำหรับข้อมูลเชิงทิศทางหรือบนแมนิโฟลด์ที่น่าสนใจ ประกอบด้วย
- Fisher, R. (1953) “Dispersion on a sphere” Proceedings of the Royal Society A 217 (20) pp.295-305.
- Mardia, K. V., Jupp, P. E. (2000) Directional Statistics, John Wiley & Sons.
- Gatto, R., Jammalamadaka, S. R. (2015) “Directional Statistics: Introduction” Wiley StatsRef: Statistics Reference Online, pp. 1-8.
1.2 ข้อมูลรูปทรง (Shape Data)
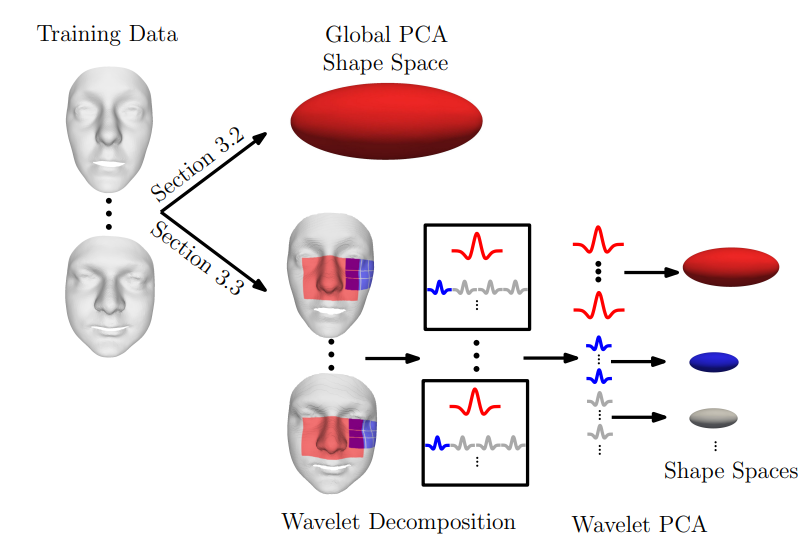
รูปที่ 10 การตรวจจับใบหน้าซึ่งอาจใช้วิธีการต่าง ๆ ได้ เช่น Convolutional Neural Networks (CNN) หรือ Principal Component Analysis (PCA) บนข้อมูลใบหน้า 2/3 มิติ30
จากที่เราพูดถึงข้อมูลบนปริภูมิที่มีลักษณะเป็นแมนิโฟลด์ปิดอย่างข้อมูลเชิงทิศทาง เราจะพูดถึงข้อมูลอีกชนิดหนึ่งที่ใช้ในชีวิตจริงโดยวางตัวอยู่บนปริภูมิยูคลิด (Euclidean space) คือ ข้อมูลรูปร่าง/รูปทรง ซึ่งตัวอย่างที่มีการนำไปใช้จริงประกอบด้วยข้อมูลดังต่อไปนี้
- การตรวจจับใบหน้า: ข้อมูลมีลักษณะเป็นรูปร่าง 2 หรือ 3 มิติก็ได้ ซึ่งในงานวิจัยสำหรับข้อมูลใบหน้า 3 มิติอาจใช้เป็น Wavelet transform แล้วลดมิติลงโดยการใช้ Principal Component Analysis30
- แบบจำลองอาคาร (Building Information Model): สามารถนำไปใช้ในการนำทางในอาคารที่สั้นที่สุดได้และนำไปใช้ในการตรวจสอบมาตรฐานโครงสร้างอาคารได้31
- ข้อมูลภูมิสารสนเทศ: เป็นข้อมูลที่สำคัญชุดหนึ่งในการตัดสินใจเชิงนโยบายอย่างมาก โดยเฉพาะการบริหารจัดการเชิงพื้นที่ ซึ่งมีเนื้อหารายละเอียดเป็นจำนวนมากในการสนใจทั้งในทางการเมือง ทางคณิตศาสตร์ และทางสังคม
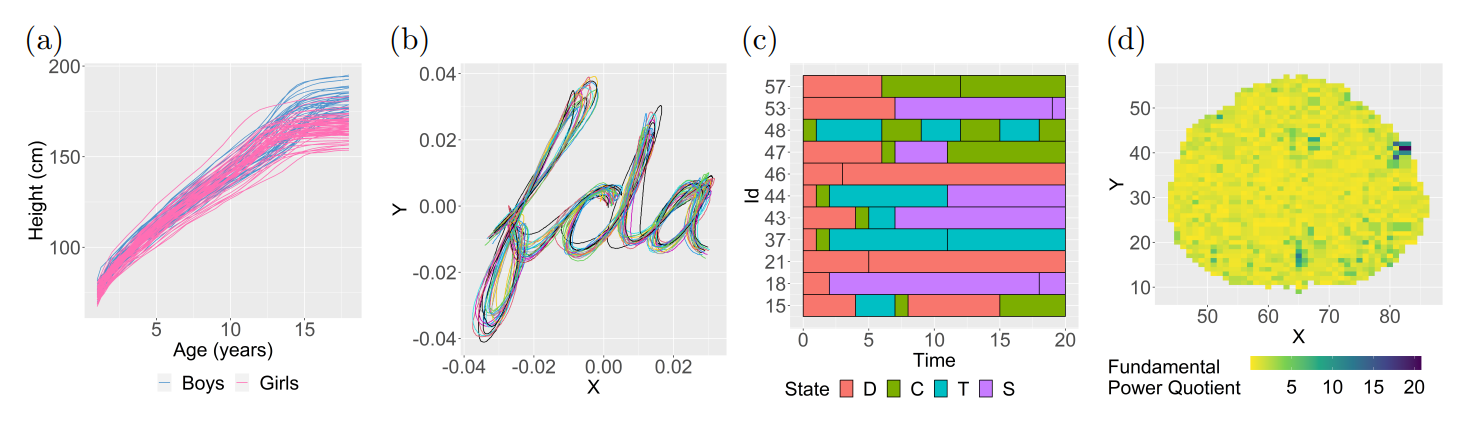
รูปที่ 11 ตัวอย่างข้อมูลเชิงฟังก์ชัน โดย (a) คือข้อมูลเชิงแนวโน้มเวลา (b) ข้อมูลลายมือ (c) ข้อมูลเชิงประเภท (d) ภาพ MRI32
เราอาจมองเป็นว่าข้อมูลรูปร่างใช้ในทางสถิติ คือ ข้อมูลเชิงฟังก์ชัน (functional data) ซึ่งหมายถึง ข้อมูลที่มองเป็นฟังก์ชัน โดยอาจมองข้อมูลอย่างข้อมูลสัญญาณ ข้อมูลรูปร่าง ข้อมูลสามมิติเป็นข้อมูลเชิงฟังก์ชันก็ได้33 โดยศาสตร์ที่เกี่ยวข้องเรียกว่า “การวิเคราะห์ข้อมูลเชิงฟังก์ชัน” (Functional data analysis) โดยเครื่องมือที่เกี่ยวข้องกับตัวแปรสุ่ม เช่น ค่าความคาดหวัง หรือ ความแปรปรวน จะถูกมองในลักษณะของฟังก์ชัน
โดยตำราหรือบทความที่แนะนำสำหรับข้อมูลเชิงฟังก์ชัน ประกอบด้วย
- Ramsay, J.O., Silverman, B.W. (2005) Functional Data Analysis 2e, Springer.
- Dabo-Niang S., Frévent C. (2024) Uncovering Data Across Continua: An Introduction to Functional Data Analysis, ArXiv: 2404.16598
- Gertheiss, J., Rügamer, D., Liew, B. X. W., Greven, S. (2024) “Functional Data Analysis: An Introduction and Recent Developments” Biometrical Journal 66 (7) pp. 1-32.
- Arlinghaus, S.L., Kerski, J.J. (2014) Spatial Mathematics: Theory and Practice through Mapping 1e, CRC Press.
1.3 ข้อมูลโครงข่าย (Network Data)
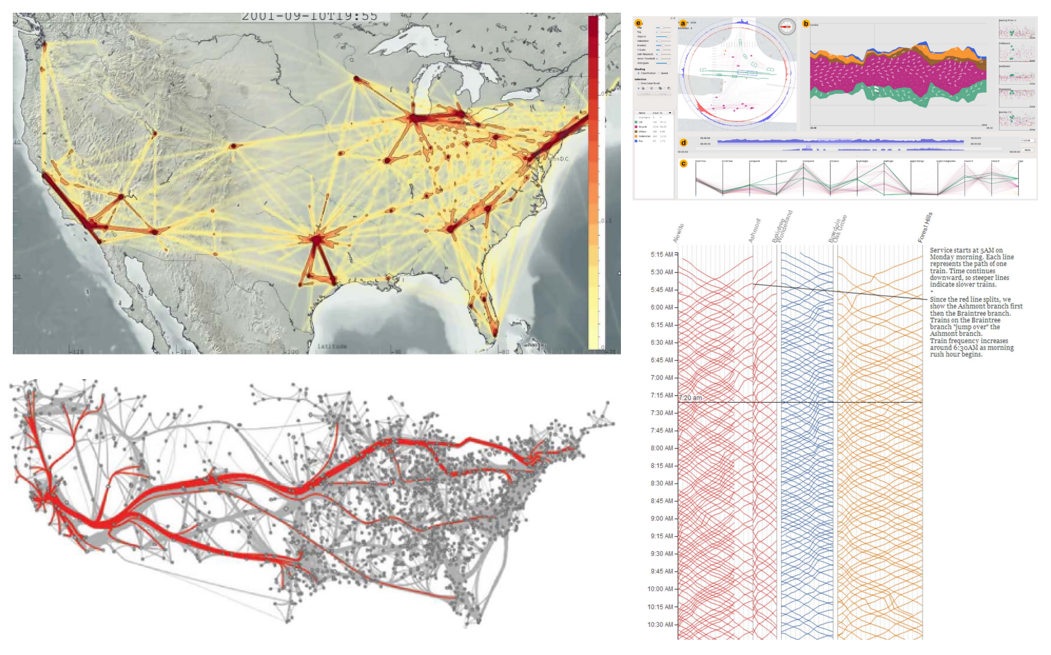
รูปที่ 12 ตัวอย่างข้อมูลโครงข่าย: สภาพการจราจรบนท้องถนน ซึ่งสังเคราะห์ข้อมูลจากการเคลื่อนที่ของรถบนท้องถนนและการควบคุมไฟจราจรในแยก34
นอกจากข้อมูลที่มีโดเมนเป็นแมนิโฟลด์หรือข้อมูลที่มีลักษณะเป็นฟังก์ชันแล้ว ข้อมูลอาจมีลักษณะเป็นโครงข่ายหรือกราฟ (graph) ก็ได้
นิยาม 3 (กราฟ) เซต $G = (V, E)$ เรียกว่า “กราฟ” โดยที่ $V$ คือ เซตของจุดยอด (vertex) และ $E$ คือ เซตของโหนด (vertex/node) โดย $E \subseteq V \times V$
รูปที่ 13 ภาพของกราฟตามนิยาม 3 โดยจุดยอดแสดงเป็นวงกลม ส่วนโหนดแสดงเป็นเส้นเชื่อมต่อระหว่างวงกลม
อ้างอิง: Undirected - Sopoforic
โดยข้อมูลกราฟมีความสำคัญอย่างมากในการวิเคราะห์ระบบพลวัต (Dynamical systems) และมีข้อมูลหลายประเภทเป็นอย่างมากที่ใช้ข้อมูลประเภทนี้ ซึ่งตัวอย่างการใช้ข้อมูลมีดังต่อไปนี้
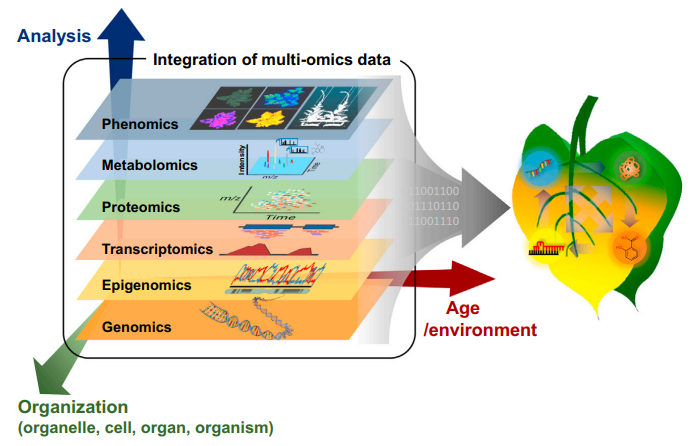
รูปที่ 14 ภาพของโอมิกส์ต่าง ๆ ในแต่ละชั้นความซับซ้อนตามชีววิทยา35
- ข้อมูลทางชีววิทยา: ข้อมูลประเภทนี้จะเป็นการเชื่อมโยงระหว่างวัตถุทางชีววิทยา เช่น ยีน เอนไซม์ หรือสารเคมีในกระบวนการเมทาบอลิซึม ซึ่งเรียกว่า โอมิกส์ (Omics) โดยศาสตร์ที่เกี่ยวข้อง คือ จีโนมิกส์ (Genomics) โปรตีโอมิกส์ (Proteomics) เมทาโบโลมิกส์ (Metabolomics) ตามลำดับ นอกจากนี้ยังมีศาสตร์โอมิกส์อื่นที่เกี่ยวข้อง เช่น มัลติโอมิกส์ (Multiomics) หรือฟลักโซมิกส์ (Fluxomics) หรือแม้แต่ข้อมูลการสอบสวนโรค ข้อมูลวิวัฒนาการ
- ข้อมูลการจราจร: ข้อมูลประเภทนี้อาจมองเป็นถนนกับแยกประกอบรวมกันเป็นกราฟ36 ซึ่งสามารถนำไปใช้ในการหาระยะทางใกล้ที่สุด (Shortest path algorithm) การหาต้นไม้ครอบคลุมขั้นต่ำ (Minimum spanning tree) เพื่อคำนวณต้นทุนต่ำสุดสำหรับการสร้างทางหลวง37
- ข้อมูลทางสังคมและประชากร: ข้อมูลประเภทนี้เป็นข้อมูลที่อยู่เป็นฐานของวิทยาศาสตร์ข้อมูลทางสังคม (Social Data Science) โดยพยายามหาลักษณะพลวัตทางสังคม ซึ่งมีข้อมูลพิสูจน์ว่าสามารถนำวิทยาศาสตร์ข้อมูลในการชักนำสังคมผ่านการเลือกตั้งดังที่กรณี Facebook-Cambridge Analytica ซึ่งก่อให้เกิดเหตุปัญหาของความเป็นส่วนบุคคลของข้อมูล
โดยตำราหรือบทความที่แนะนำสำหรับข้อมูลโครงข่ายประกอบด้วย
- Kalyagin, V. A., Koldanov, A. P., Koldanov, P. A., Pardalos, P. M. (2020) Statistical Analysis of Graph Structures in Random Variable Networks, Springer.
- Brandes, U., Erlebach, T. (2005) Network Analysis: Methodological Foundations, Springer.
- Dabke, D.V. (2023) On Systems of Dynamic Graph: Theory and Applications, Doctor of Philosophy’s Dissertation, Princeton University.
- Fiedler, B., Mochizuki, A., Kurosawa, G., Saito, D. (2013) “Dynamics and control at feedback vertex sets. I: Informative and determining nodes in regulatory networks” Journal of Dynamics and Differential Equations 25, pp.563-604. (Part I, Part II)
ความประหลาดแบบที่ 2: ข้อมูลอาจไม่เพียงพอ
โดยปกติแล้ว อุดมคติของข้อมูลสำหรับการวิเคราะห์อาจต้องมีคุณสมบัติที่สมบูรณ์ครบถ้วนทุกค่า มีจำนวนสมาชิกแต่ละกลุ่มใกล้เคียงกัน หรือสามารถเก็บข้อมูลได้ตลอด แต่บางทีข้อมูลอาจไม่เป็นแบบนั้น
2.1 ข้อมูลที่หายไป (Missing Data)
ข้อมูลอาจไม่ได้มีความสมบูรณ์นักเนื่องจากอุปสรรคในการเก็บข้อมูล นักสถิติจึงมีการศึกษาเกี่ยวกับเรื่องนี้เรียกว่า “แบบจำลองกึ่งอิงพารามิเตอร์” (Semiparametric models) ซึ่งครอบคลุมทั้งข้อมูลสูญหายและข้อมูลระยะปลอดเหตุการณ์ (Survival data) และอาจมีวิธีการอื่นที่เกี่ยวข้อง โดยอิงจากหนังสือตำราและบทความดังต่อไปนี้
- Tsiatis, A.A. (2006) Semiparametric Theory and Missing Data, Springer.
- Kleinke, K., Reinecke, J., Salfrán, D., Spiess, M. (2010) Applied Multiple Imputation: Advantages, Pitfalls, New Developments and Applications in R, Springer.
- Kleinbaum, D. G., Klein, M. (2012) Survival Analysis: A Self-Learning Text, Springer.
2.2 ข้อมูลไม่สมดุล (Imbalanced Data)
ข้อมูลที่ไม่สมดุลอาจมีปัญหาในการคัดแยก (Classification) ซึ่งไม่ได้เป็นปัญหาที่มีนัยสำคัญในงานสถิติ แต่เป็นงานในทางปัญญาประดิษฐ์ เราไม่สามารถเรียนรู้ลักษณะความแตกต่างระหว่าง class ในการคัดแยกได้อย่างชัดเจน โดยอาจมองเป็นประเภทการวิเคราะห์ออกเป็นสองแบบ คือ การเติมข้อมูลให้ความไม่สมดุลของ class ให้สมดุล กับ การวิเคราะห์ความผิดปกติ โดยอิงจากหนังสือตำราและบทความดังต่อไปนี้
- Fernández, A., García, S., Galar, M., Prati, R.C., Krawczyk, B., Herrera, F. (2018) Learning from Imbalanced Data Sets, Springer.
- Mehrotra, K. G., Mohan, C. K., Huang, H. (2019) Anomaly Detection Principles and Algorithms, Springer.
ความประหลาดแบบที่ 3: การสังเคราะห์ความรู้จากภาพใหญ่ของข้อมูล
เราอาจเคยได้ยินว่า “Correlation does not imply causation.” (สหสัมพันธ์ไม่ได้หมายถึงความสัมพันธ์) แต่ทว่าก็มีนักสถิติมีการศึกษาทางสถิติเพื่อหาความสัมพันธ์ที่แท้จริงออกมาดังต่อไปนี้
3.1 การหาเหตุผลในข้อมูล (Causal Analysis)
การวิเคราะห์เหตุผลในข้อมูลเป็นศาสตร์ที่พยายามหาเหตุและผลที่แท้จริง โดยกระบวนการหาเหตุผลในทางสถิติเรียกว่า “การอนุมานเหตุผล” (Causal Inference) ซึ่งมีเครื่องมือในการศึกษาจำนวนมาก อาทิ ทฤษฎีกราฟ แบบจำลองสมการโครงสร้าง (Structural Equation Modeling) และแบบจำลองเชิงเส้นทั่วไป (Generalized Linear Model)โดยหนังสือตำราและบทความที่เกี่ยวข้องที่น่าสนใจอาจพิจารณาจากสิ่งเหล่านี้
- Pearl, J. (2009) “Causal inference in statistics: An overview” Statistical Surveys 3 pp. 96-146. (DOI: 10.1214/09-SS057)
- Wager, S. (2024) Causal Inference: A Statistical Learning Approach (Available here)
3.2 ข้อมูลเชิงสัญลักษณ์ (Symbolic Data)
บางครั้งข้อมูลอาจไม่ได้เป็นข้อมูลเดี่ยว ๆ แต่อาจเป็นเซตหรือวัตถุทางคณิตศาสตร์อื่นใด ซึ่งแสดงให้เห็นถึงภาพทั้งหมดของข้อมูลชุดหนึ่ง โดยในการประมวลผลข้อมูลส่วนบุคคลจะเรียกว่า การทำโปรไฟล์ผู้ใช้ (Data profiling)
หนังสือตำราและบทความที่เกี่ยวข้องที่น่าสนใจอาจพิจารณาจากสิ่งเหล่านี้
- Billard, L., Diday, E. (2003) “From the Statistics of Data to the Statistics of Knowledge: Symbolic Data Analysis”, Journal of the American Statistical Association 98 (462) pp. 470-487.
- Billard, L., Diday, E. (2003) Symbolic Data Analysis: Definitions and Examples.
- Brito, P., Silva, A. P. D. (2025) “Parametric models for distributional data” Advances in Data Analysis and Classification, Springer.
- Amari, S. (2016) Information Geometry and Its Applications, Springer.
นอกจากนี้แล้ว อาจมีข้อมูลในรูปแบบลักษณะอื่นที่เราไม่ได้เขียนไว้ ณ ที่นี้ ซึ่งเราจะรวบรวมมาทีหลังพร้อมเขียนรายละเอียดที่เกี่ยวข้องให้เพียงพอกับความเข้าใจในข้อมูลชุดต่าง ๆ เหล่านั้นในตอนต่อไป
เชิงอรรถ
-
วิธีการแบ่งประเภทของข้อมูลมักจะปรากฎอยู่เป็นการทั่วไป เช่น วิชาที่เกี่ยวกับวิทยาการข้อมูล, บทความที่เกี่ยวกับวิทยาการข้อมูล หรือ วิชาทางสถิติ ↩
-
(ย่อ: SSS (1946)) Stevens S. S. (1946) “On the Theory of Scales and Measurement”, Science 103 (2684) pp. 677-680. ↩
-
อ้างอิงจากสรุปงานเขียนของ Leary, D.E. (1982) “Immanuel Kant and the Development of Modern Psychology” The Problematic Science: Psychology in Nineteenth-Century Thought p.22. ↩
-
Dzhafarov, E. N., Colonius, H. (2011) “The Fechnerian Idea” The American Journal of Psychology 124 (2), pp. 127-140. ↩
-
(ย่อ: Pickren and Rutherford (2010)) Pickren, W.E., Rutherford, A. (2010) A history of modern psychology in context, Wiley & Sons Inc., New Jersey, p.25. ↩
-
ปัจจุบันการดูโหงวเฮ้งและการพยากรณ์โรคจากลักษณะกระโหลกศีรษะได้ถูกมองว่าเป็นวิทยาศาสตร์เทียม (Pseudoscience) สามารถอ่านได้เพิ่มเติมจาก Physiognomy, Photography and the criminal look ว่าศาสตร์ของโหงวเฮ้งถูกพยายามนำมาใช้ในงานอาชญวิทยา ซึ่งทำโดยเซอร์ฟรานเซส กัลตัน (Sir Frances Galton, 1822-1911) พบว่าไม่สามารถเชื่อมโยงโหงวเฮ้งกับพฤติกรรมการเป็นอาชญากรได้แต่อย่างใด ↩
-
Pickren and Rutherford (2010), p.49. ↩
-
Michell J. (1990) An Introduction To the Logic of Psychological Measurement 1e, Psychology Press, pp.8-9. ↩
-
(ย่อ: BAAS (1932)) British Association for the Advancement of Science (1932) Report of the Annual Meeting, 1932 (102nd Year), Office of the British Association, Burlington House, London, pp.300-302. ↩
-
สามารถหาพบรายงานนั้นได้ที่หอจดหมายเหตุมหาวิทยาลัยเคมบริดจ์ โดยอ้างอิงเนื้อหาจากบทความของสตีเฟนส์เองใน SSS (1946), p.677. ↩
-
SSS (1946), p.680. ↩
-
SSS (1946), p.678, Table 1. ↩
-
Illowsky, B., Dean, S. (2013) Introductory Statistics OpenStax, Houston, Texas. Chapter 1.3. (Available here) ↩
-
Lane, D. M. (1993) HyperStat (Online) Chapter 1.6. (Available here) ↩
-
Gravetter, F. J., Wallnau, L. B. (2015) Statistics for the Behavioral Sciences 10e, Cengage Learning, Boston, Massachusetts, pp.18-24. ↩
-
(ย่อ: Velleman and Wilkinson (1993)) Velleman, P. F., Wilkinson, L. (1993) “Nominal, Ordinal, Interval, and Ratio Typology Are Misleading” The American Statistician 47 (1), pp.65-72. ↩
-
Velleman and Wilkinson (1993), p.67. ↩
-
Velleman and Wilkinson (1993), p.71. ↩
-
Mosteller, Frederick; Tukey, John W. (1977). Data analysis and regression: a second course in statistics. Reading, Mass: Addison-Wesley Pub. Co. ↩
-
(ย่อ: Chrisman (1998)) Chrisman, N. R. (1998) “Rethinking Levels of Measurement for Cartography”, Cartography and Geographic Information Systems 25 (4), pp. 231-242. ↩
-
Chrisman (1998), p.239 Fig.3. ↩
-
ข้อมูลราคาเป็นข้อมูลไม่ต่อเนื่องในความเป็นจริง เนื่องจากราคาอยู่บนฐานของสกุลเงิน ซึ่งแบ่งเป็นหน่วยย่อยที่สุด เช่น สตางค์ในสกุลบาทไทย เซนต์ในสกุลดอลลาร์ ↩
-
จากทฤษฎีบทการจำแนกระบุว่า $2$-manifold สามารถจำแนกออกได้เป็น $\mathbb{S}^2$, connected sum ของ $\mathbb{T}^2$ และ connected sum ของ $\mathbb{P}^2$ (อ่านเพิ่มเติมที่ทฤษฎีบท 4.14 ของ Kinsey L.C. (1991) Topology of Surfaces, Undergraduate texts in mathematics, Springer-Verlag, New York pp.79-85.) แต่ทว่าการจำแนกของ $n$-manifold อาจไม่ได้มีลักษณะแบบนี้ ซึ่งการศึกษาของการจำแนกเหล่านี้จะอยู่ในรายวิชา “ทอพอโลยีเชิงอนุพันธ์” (Differential Topology) ↩
-
Bowers, J.A., Morton, I.D., Mould, G.I. (2000) “Directional statistics of the wind and waves” Applied Ocean Research 22 pp.13-30. ↩
-
Arnold, B.C., SenGupta A. (2006) “Recent advances in the analyses of directional data in ecological and environmental sciences” Environ Ecol Stat 13, pp. 253-256. ↩
-
Wiechers, H., Eltzner, B., Mardia, K.V., Huckemann, S.F. (2023) “Learning torus PCA-based classification for multiscale RNA correction with application to SARS-CoV-2”, Journal of the Royal Statistical Sociery Series C: Applied Statistics 72, pp. 271-293. ↩
-
Sittel, F., Filk, T., Stock, G. (2017) “Principal component analysis on a torus: Theory and application to protein dynamics”, The Journal of chemical physics 147 (Available here) ↩
-
Patricia, L., Morellato, C., Alberti, L.F., Hudson, I.L. (2010) “Applications of Circular Statistics in Plant Phenology: a Case Studies Approach” Phenological Research, Springer Science+Business Media, pp. 339-359. (DOI: 10.1007/978-90-481-3335-2_16) ↩
-
Gill, J., Hangartner, D. (2010) “Circular Data in Political Science and How to Handle It”, Political Analysis 18, pp. 316-336. ↩
-
Brunton, A., Salazar, A., Bolkart, T., Wuhrer, S. (2014) Review of Statistical Shape Spaces for 3D Data with Comparative Analysis for Human Faces, ArXiv: 1209.6491. ↩
-
Zhou, Y. W., Hu, Z. Z., Lin, J. R., Zhang, J. P. (2020) “A Review on 3D Spatial Data Analytics for Building Information Models” Archives of Computational Methods in Engineering 27, pp. 1449-1463. ↩
-
Dabo-Niang S., Frévent C. (2024) Uncovering Data Across Continua: An Introduction to Functional Data Analysis, ArXiv: 2404.16598 ↩
-
Gertheiss, J., Rügamer, D., Liew, B. X. W., Greven, S. (2024) “Functional Data Analysis: An Introduction and Recent Developments” Biometrical Journal 66 (7) pp. 1-32. ↩
-
Chen, W., Guo, F., Wang, F.Y. (2015) “A Survey of Traffic Data Visualization” IEEE Transactions on Intelligent Transportation Systems 16 (6) pp. 2970-2984. ↩
-
Kim, J., Woo, H. R., Nam, H. G. (2016) “Toward Systems Understanding of Leaf Senescence: An Integrated Multi-Omics Perspective on Leaf Senescence Research”, Molecular Plant 9, pp. 813-825. (DOI: 10.1016/j.molp.2016.04.017) ↩
-
Thomson, R. C., Richardson, D. E. (1995) “A Graph Theory Approach to Road Network Generalization” 17th International Cartographic Conference-10th General Assembly of ICA, Proceedings, pp. 1871-1880. ↩
-
Effanga, E. O., Edeke, U. E. (2016) “Minimum Spanning Tree of City to City Road Network in Nigeria” IOSR Journal of Mathematics 12 (4), pp.41-45. ↩